价格敏感度模型之因子分析

模型思路：价格敏感度模型是根据业务需求，将用户划分为3-5类。比如极度敏感、重度敏感、较敏感、一般敏感、不敏感等。然后在发放优惠券的时候，根据场景+用户价格敏感度标签等组合，确定人群类别，提升钱效的使用效率。

步骤：先根据实际业务，找出所有可能影响因子，将其聚类划分成3-5类。根据预测分类结果，将预测结果所有的列指标求平均，然后相加。根据结果数值大小，从高到低排序，将其划分为极度敏感、重度敏感、较敏感、一般敏感、不敏感等标签（注意这里的指标必须跟预测结果正向，如果不正向需要将指标进行转换）。

因子分析法的主要步骤如下：

导入数据预处理
计算样本的相关矩阵
样本进行标准化处理
求相关矩阵R的特征值、特征向量
根据系统要求的累积贡献度确定主因子的个数
计算因子载荷矩阵A
最终确定因子模型

一、数据预处理

1.1、首先进行数据导入

查看样式、数据描述，代码和结果如下：

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
data=pd.read_excel("C:/Users/10851/Desktop/product_price_sensetive_v.xls")
print(data.head())
#因子分析对极端值比较敏感，需要先考察是否存在极端值
print(data.describe())
print(data.info())

data.head()表现如下：

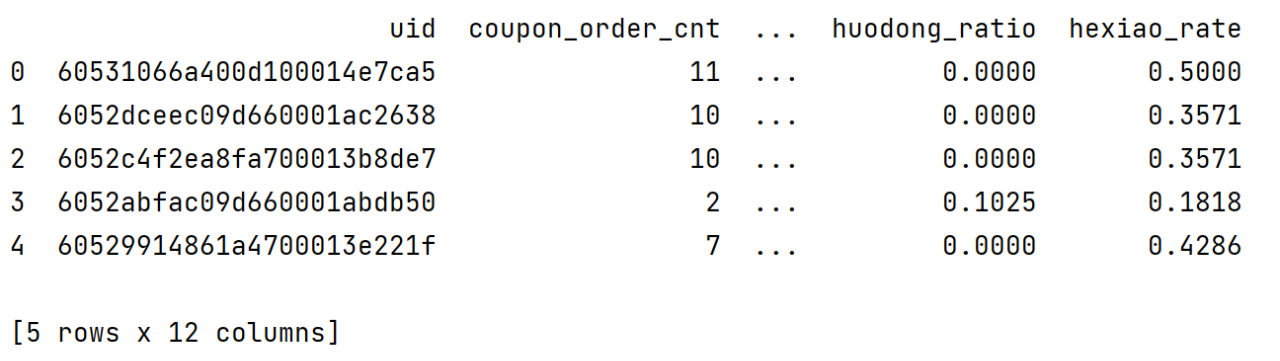data.describe()可以看到各个指标个数、平均值、标准差、极小值、前25%、前50%、前75%、极大值。因子分析的结果对变量中的极端值比较敏感，因此事先观察数据中是否存在极端值很有必要。

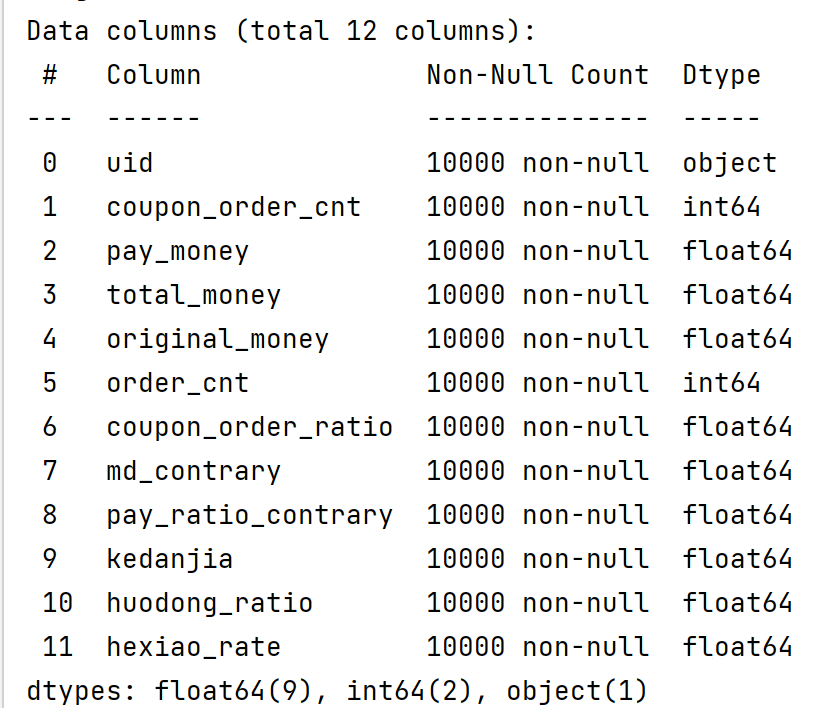
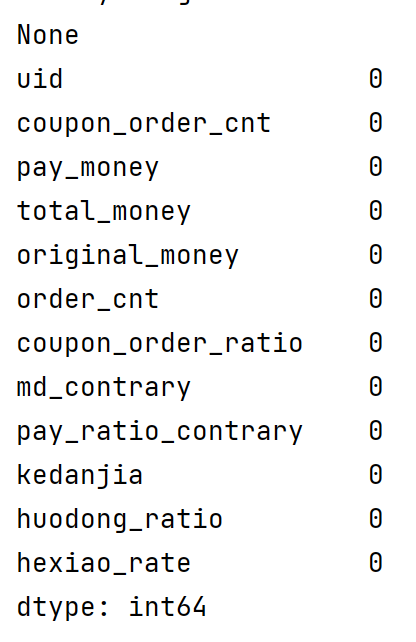
1.2、查看数据的缺失值

大部分数据是存在缺失值，一般采用如下方式查看：

pint(data.isnull().sum())

1.3、数据预处理

数据预处理包含去除无效的字段（对分析没有任何作用），同时去掉存在空值的数据：

data.drop(["coupon_order_cnt","pay_money","total_money","original_money","order_cnt","kedanjia"],axis=1,inplace=True)
print(data.info())

# 去掉空值
data.dropna(inplace=True)

二、相关性分析

data_df=pd.DataFrame(data,columns["discount_ratio","coupon_order_ratio","md_contrary","pay_ratio_contrary","huodong_ratio","hexiao_rate"])

sns.heatmap(data_df.corr(),annot=True,cmap="YlGnBu")

plt.xticks(fontsize=5,rotation=360)

plt.yticks(fontsize=5)

plt.show()

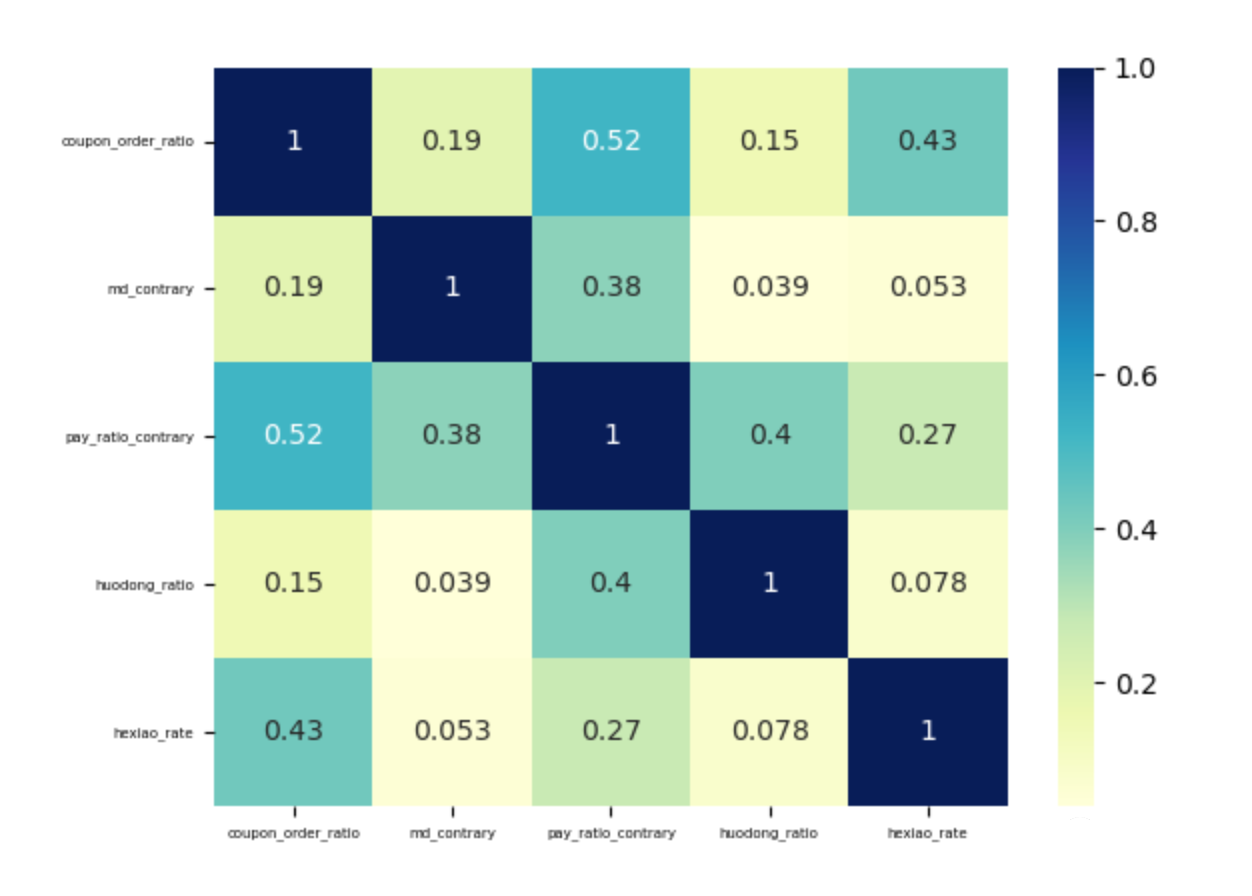
三、建模过程

3.1、充分性检查

在进行因子分析之前，需要先进行充分性检测，主要是检验相关特征阵中各个变量间的相关性，是否为单位矩阵，也就是检验各个变量是否各自独立。通常是两种方法：

KMO检验
Bartlett's球状检验（巴特利球形检验）

KMO检验

检查变量间的相关性和偏相关性，取值在0-1之间；KOM统计量越接近1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。

通常取值从0.6开始进行因子分析。本案例为0.60，所以尚可以接受。

kmo_all,kmo_model=calculate_kmo(data_df) # kmo值要大于0.6
print(kmo_all)
print(kmo_model)

Bartlett's球状检验

检验总体变量的相关矩阵是否是单位阵（相关系数矩阵对角线的所有元素均为1,所有非对角线上的元素均为零）；即检验各个变量是否各自独立。

如果不是单位矩阵，说明原变量之间存在相关性，可以进行因子分析；反之，原变量之间不存在相关性，数据不适合进行主成分分析。

bartlett = calculate_bartlett_sphericity(data_df) # bartlett球形度检验p值要小于0.05
print(bartlett)

我们发现统计量p-value的值为0，表明变量的相关矩阵不是单位矩阵，即各个变量之间是存在一定的相关性，我们就可以进行因子分析。

#(8698.300915006257, 0.0)

3.2、求相关矩阵R的特征值、特征向量

在数据说明中，我们已经知道了这些变量是和5个隐藏的因子相关。但是很多情况下，我们并不知道个数，需要自己进行探索。

方法：肘部法则、轮廓系数等。本文使用肘部法则，肘部法则只能使用PYTHON实现，无法使用SPSS。

3.2、特征值和特征向量

确定公因子个数的一般标准：特征值大于1或累计方差贡献率大于85%(此值可根据实际数据酌情更改)。

print("输出特征值ev、特征向量v")
faa = FactorAnalyzer(5,rotation=None)
faa.fit(data_df)
ev,v=faa.get_eigenvalues()
print(ev)
print(v)

ratation参数的其他取值情况：

varimax (orthogonal rotation)

promax (oblique rotation)

oblimin (oblique rotation)

oblimax (orthogonal rotation)

quartimin (oblique rotation)

quartimax (orthogonal rotation)

equamax (orthogonal rotation)

输出特征值ev、特征向量v

[2.87185753 1.03661165 0.96965399 0.6012702 0.44623177 0.07437486]

[ 2.65173802e+00 4.88661933e-01 2.77728301e-01 3.14829509e-021.60615868e-02 -9.72298553e-06]

3.3、查看因子贡献率-get_factor_variance()

通过理论部分的解释，我们发现每个因子都对变量有一定的贡献，存在某个贡献度的值，在这里查看3个和贡献度相关的指标：

总方差贡献：variance (numpy array) – The factor variances

方差贡献率：proportional_variance (numpy array) – The proportional factor variances

累积方差贡献率：cumulative_variances (numpy array) – The cumulative factor variances

print("输出累计方差贡献率")
var=faa.get_factor_variance()
print(var[0])
print(var[1])
print(var[2])

输出累计方差贡献率

[2.65173615 0.48865974 0.27772628 0.03148149 0.01605941]

[0.44195602 0.08144329 0.04628771 0.00524691 0.00267657]

[0.44195602 0.52339932 0.56968703 0.57493394 0.57761051]

3.4、可视化展示

numeric_cols=["discount_ratio","coupon_order_ratio","md_contrary","pay_ratio_contrary","huodong_ratio","hexiao_rate"]
numeric_col_means = data_df.loc[:, numeric_cols].mean()
numeric_col_std = data_df.loc[:, numeric_cols].std()
data_df.loc[:, numeric_cols] = (data_df.loc[:, numeric_cols] - numeric_col_means) / numeric_col_std

SSE = [] # 存放每次结果的误差平方和
for k in range(2,12):
estimator = KMeans(n_clusters=k) # 构造聚类器
estimator.fit(data.loc[:,numeric_cols])
SSE.append(estimator.inertia_) # estimator.inertia_获取聚类准则的总和
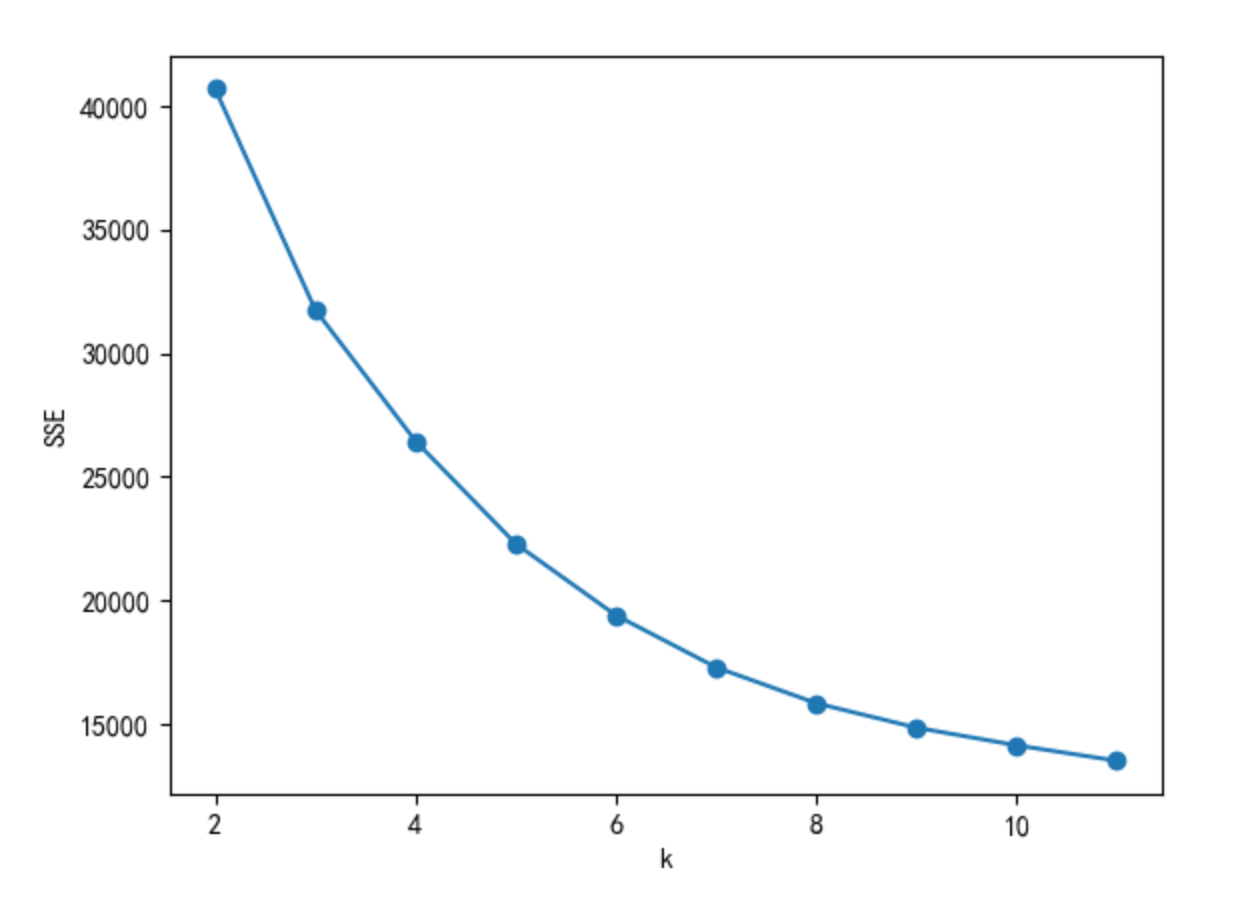
X = range(2,12)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.show()

我们将特征值和因子个数的变化绘制成图形：

3.5、因子载荷矩阵

我们选择5个因子来进行因子分子的建模过程，

faa_result=faa.fit(data_df)
print(faa_result)
print("因子载荷矩阵: ", faa_result.loadings_)

FactorAnalyzer(n_factors=5, rotation=None, rotation_kwargs={})

因子载荷矩阵:

[[ 0.9557582 -0.10564533 -0.12595834 -0.12479756 -0.01296434]

[ 0.64564377 0.39795808 -0.0249669 -0.00225015 0.07575553]

[ 0.38617468 -0.16988455 -0.31280392 0.0979549 0.03687305]

[ 0.95487265 -0.22769584 0.11062269 0.06394198 -0.04778007]

[ 0.33551995 -0.15288432 0.38426096 0.013325 0.05370993]

[ 0.384604 0.46373312 0.05913771 0.04517408 -0.06020899]]

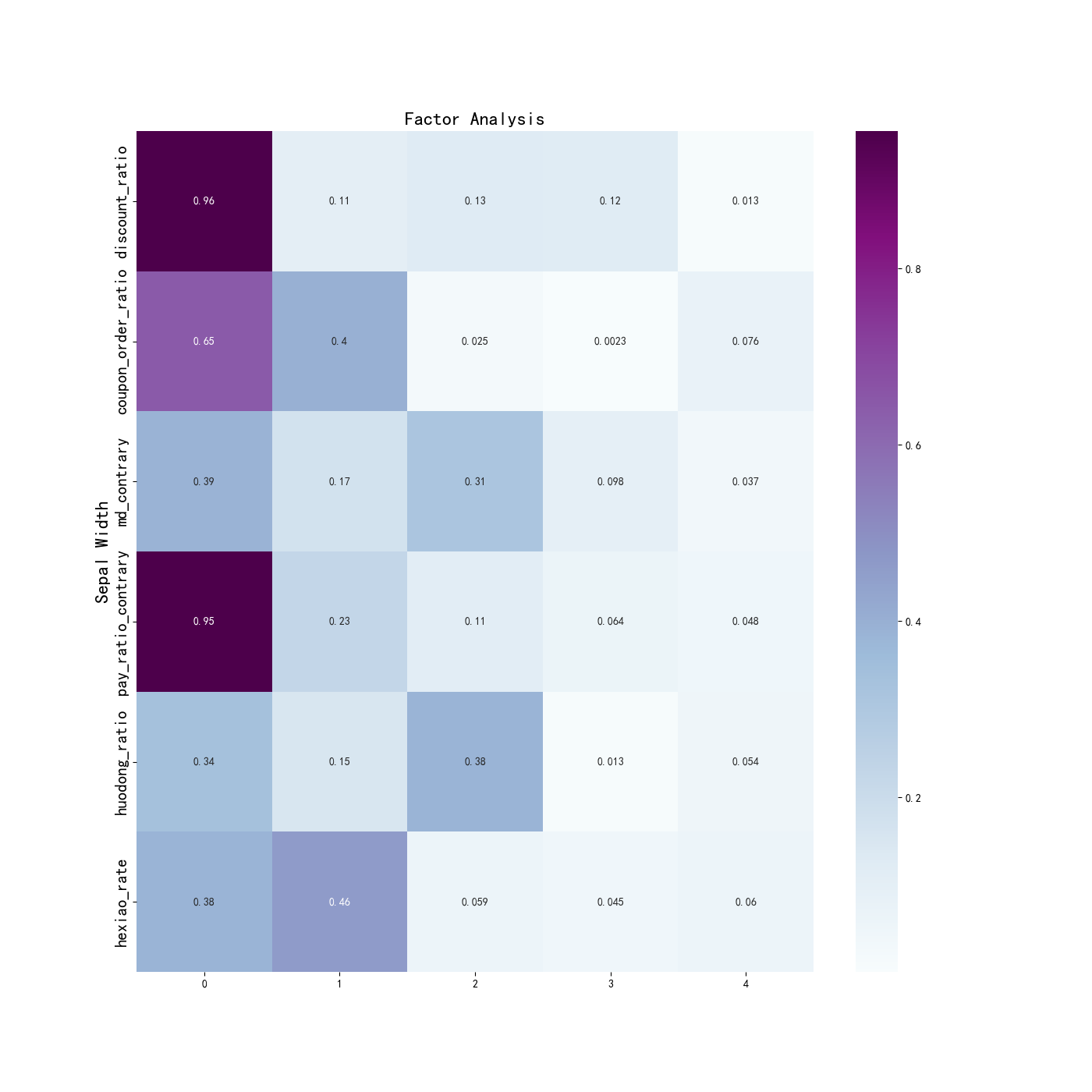
3.6、变量可视化

为了更直观地观察每个隐藏变量和哪些特征的关系比较大，进行可视化展示，为了方便取上面相关系数的绝对值：

# 绘图
df_cm = pd.DataFrame(np.abs(faa.loadings_), index=data_df.columns)
print(df_cm)
plt.figure(figsize = (14,14))
ax = sns.heatmap(df_cm, annot=True, cmap="BuPu")
# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")
# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()
plt.savefig("C:/Users/10851/Desktop/factorAnalysis", dpi=500)

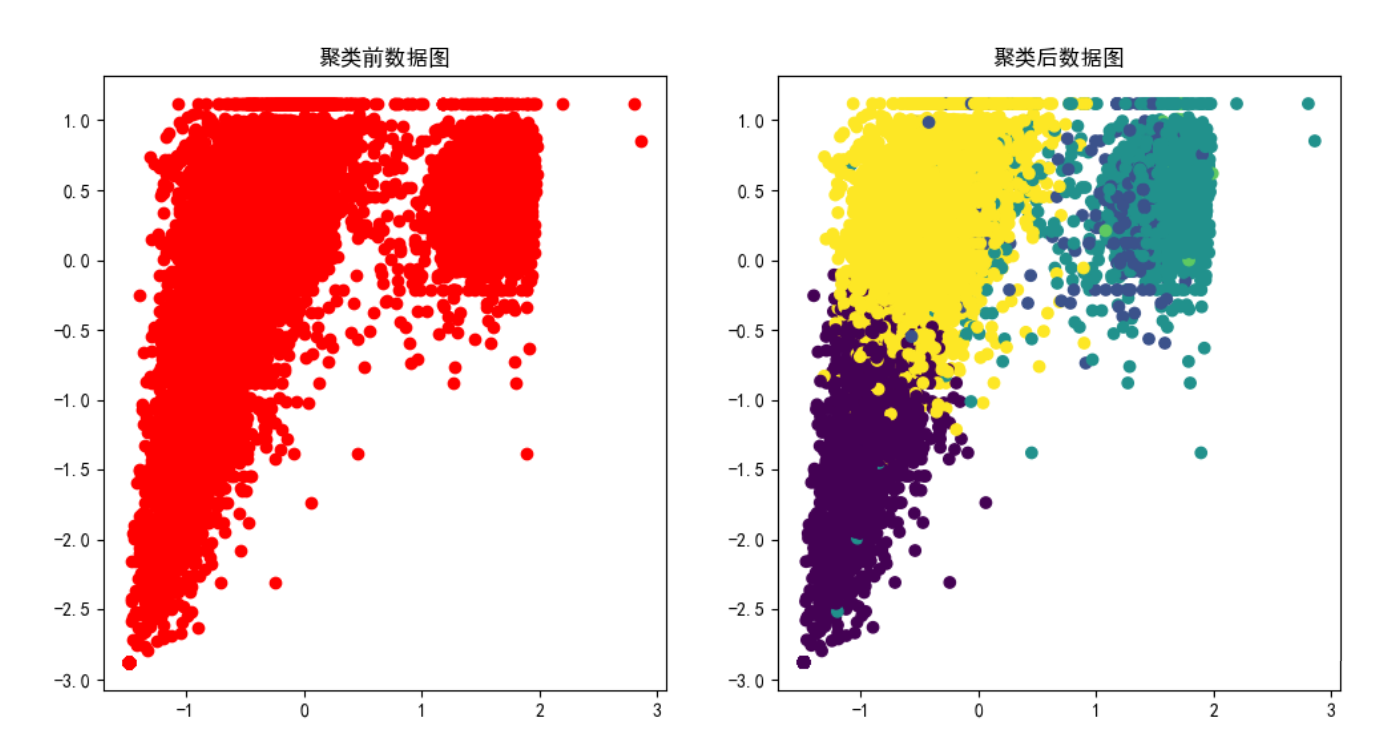
3.7、散点图

#绘制聚成几大类的散点图
data_std = StandardScaler().fit_transform(data_df) #标准化
kmeans=KMeans(n_clusters=3,random_state=170).fit(data_std)
# 获取聚类结果
labels = kmeans.labels_
# 获取聚类中心
cluster_centers = kmeans.cluster_centers_
print("聚类结果：", labels)
print("聚类中心：", cluster_centers)

plt.figure(figsize=(12,6))
plt.subplot(121)
plt.scatter(data_std[:,0],data_std[:,1],c='r')
plt.title("聚类前数据图")
plt.subplot(122)
plt.scatter(data_std[:,0],data_std[:,1],c=kmeans.labels_)
plt.title("聚类后数据图")
plt.show()

3.8、转换为新的变量

最后, 就是当我们知道使用新的5个变量比较合适之后, 我们将原始的数据都转换为5个新的特征, 转换的方式如下所示:

data_new=pd.DataFrame(faa.transform(data_df))
print(data_new)

最后输出的大小是9999*5, 也就是每一个数据都有5个特征。

3.9、聚类结果求均值

model=KMeans(n_clusters=5,max_iter=1000)
model.fit(data.loc[:,numeric_cols])
data_df["predict"]=model.predict(data_df.loc[:,numeric_cols])
print(data_df["predict"].value_counts())
clusters_means_all=data_df.groupby('predict').mean()
clusters_means_all.to_excel('C:/Users/10851/Desktop/data_julei_result.xlsx')

至此，我们完成了价格敏感度的因子分析案例。

附件

关注公众号「水沐教育科技」，在手机上阅读所有教程，随时随地都能学习。内含一款搜索神器，免费下载全网书籍和视频。

公众号二维码
微信扫码关注公众号