如何理解逻辑回归中残差诊断

如何理解机器学习中残差，下面以一个简单案例来进行解读。

 

假设我们有一个非常简单的逻辑回归模型，只有一个自变量x和一个因变量y，其形式如下：logit(p)=β0​+β1​X

其中，p表示响应变量的概率，β0​、β1​分别是截距和斜率。

对于这个模型，我们可以通过计算残差来评估它的拟合效果。残差是指模型预测值与观测值之间的差异，即：

residual = y-y^

 

其中，y是观测到的响应变量数据，y^​是模型对该数据的预测值。在逻辑回归模型中，预测值通常是一个介于0和1之间的实数，表示响应变量为1的概率。因此，我们需要将预测值转化为二元分类结果，才能计算残差。

 

具体来说，我们可以将预测值y^​与一个阈值tt进行比较，如果y^​大于t，则将响应变量y设为1，否则设为0。通常情况下，这个阈值t取0.5，但也可以根据实际情况进行调整。然后，我们可以计算残差residual的值，如果residual为正数，表示模型对这个数据的预测值过小，如果residual为负数，表示模型对这个数据的预测值过大。

 

在这个简单的逻辑回归模型中，我们可以通过计算残差的平方和来评估模型的拟合效果。具体来说，我们可以计算：

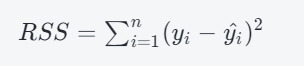
其中，n是样本容量，yi​和yi​^​分别是第i个观测数据的实际响应值和模型预测值。如果RSS的值比较小，表示模型对数据的拟合效果比较好；反之，如果RSS的值比较大，那么就需要重新检验模型的假设，或者重新修改数据和模型。

 

现在我们有一组数据，其中自变量x的取值为：x=[1,2,3,4,5]，响应变量y的取值为：y=[0,0,1,1,1]，

假设我们使用逻辑回归模型对这组数据进行拟合，得到的模型为：

logit(p) = -2 + 0.8x

现在我们想要计算预测值y^​和残差residual的值。

首先，我们需要根据模型公式计算每个x对应的预测值p^​：

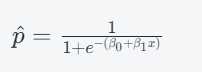
代入模型参数，我们可以计算出每个xx对应的预测值p^​：

x=1,p^​=0.27

x=2,p^​=0.47

x=3,p^​=0.71

x=4,p^​=0.89

x=5,p^​=0.97

接下来，我们需要将预测值p^​转化为二元分类结果。根据通常的做法，我们可以将阈值t设为0.5，即如果p^​≥0.5，则将响应变量y设为1，否则设为0。根据这个规则，我们可以计算出每个xx对应的预测结果y^​：

x=1,y^​=0

x=2,y^​=0

x=3,y^​=1

x=4,y^​=1

x=5,y^​=1

现在我们可以计算每个观测数据的残差residual，即：

residual =y−y^​

代入响应变量y和预测结果y^​的值，我们可以计算得到每个观测数据的残差：

x=1,residual=0−0=0

x=2,residual=0−0=0

x=3,residual=1−1=0

x=4,residual=1−1=0

x=5,residual=1−1=0

这里每个观测数据的残差都为0，表示模型对这组数据的拟合效果比较好。我们还可以计算出这组数据的残差平方和RSSRSS，即：

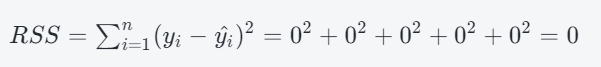
这里RSSRSS的值为0，表示模型对这组数据的拟合效果非常好，没有残差。

 

附件

关注公众号「水沐教育科技」，在手机上阅读所有教程，随时随地都能学习。内含一款搜索神器，免费下载全网书籍和视频。

微信扫码关注公众号