怎么理解logit
人们常说的“Logit模型”,这里的“Logit”到底是指什么?要回答这个问题,得先弄清楚一个概念——Odds!
1. 何为Odds?
在英语里,Odds的意思就是指几率、可能性。在统计学里,概率(Probability)和Odds都是用来描述某件事情发生的可能性的。概率描述的是某事件A出现的次数与所有结果出现的次数之比。公式表示:
P=(number of event A)/(total number of events)
概率是一个0到1之间的实数;P=0表示一定不会发生,而P=1则表示一定会发生。以掷骰子为例。掷出点数为6的概率为:
P=6
掷出点数为6的概率为:P=1/6

Odds指的是 事件发生的概率 与 事件不发生的概率 之比。公式表示为:
Odds=P/(1-P)
继续上面掷骰子的例子。出现点数6的概率 P=1/6,出现其它点数的概率 1−P=5/6。根据Odds公式可以得到掷出点数为6这一事件的Odds为:
Odds=1/6除以5/6=1/5
用更通俗的解释:平均来看,掷出6点的成功的概率和失败的概率之比为1:5。
2. Odds和概率之间的关系
换一个角度来看:可以推导出事件A的Odds 等于 事件A出现的次数 和 其它(非A)事件出现的次数 之比;
下表1和图4展示了概率P从0.01变化到0.99时,相应的Odds变化的情况。注意:(1)当概率等于0.5的时候,Odds等于1(等分);(2)概率P的变化范围是[0,1],而Odds的变化范围是[0,+∞)。再进一步,如果对Odds取自然对数,就可以将概率P从范围[0,1]映射到(−∞,+∞)。Odds的对数称之为Logit。
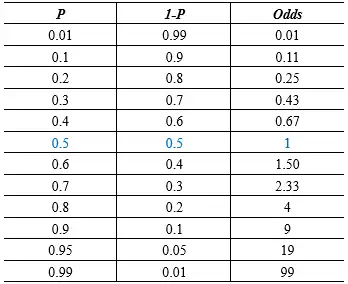
Odds和概率P之间的关系
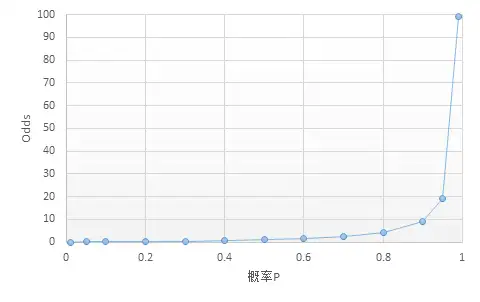
概率P和Odds之间的关系
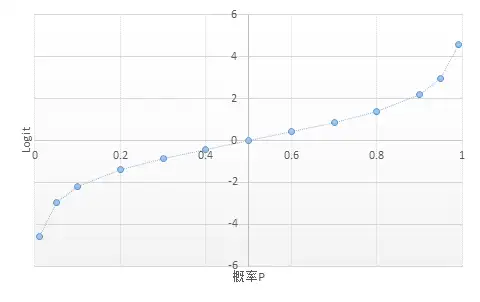
概率P和 Logit 之间的关系
这就是一个Logit变换。实际上,所谓 Logit 模型可以理解成 Log-it(即 it 的自然对数——这里的 it 指的就是Odds)。

Logit变换
与概率不同,Logit的一个很重要的特性就是没有上下限——这就给建模带来极大方便。
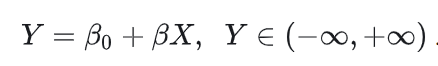
对概率P进行建模——因为左边p的取值范围是(−∞,+∞),而概率p的取值范围是[0,1]。但是,由于 Logit 和β0+βx都是在(−∞,+∞)上变化,我们可以尝试建立Logit 和β0+β1x之间的对应关系,例如:
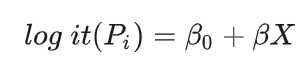
如果将x和β看成向量形式,则:
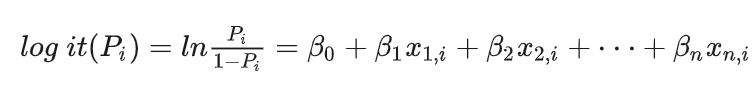
关注公众号「水沐教育科技」,在手机上阅读所有教程,随时随地都能学习。内含一款搜索神器,免费下载全网书籍和视频。

微信扫码关注公众号