卡方分布原理以及应用
首先向大家介绍基于卡方检验的方式。提到卡方检验大家应该都不陌生,卡方检验是一种用途很广的假设检验方式,属于非参检验范畴,其目的是比较理论频次与实际频次是否吻合,是否属于同一分布。
核心步骤如下:
首先:设定假设检验的 原假设H0 和 备选假设H1,和P值。
原假设H0:实际频次与期望频次没有差别。
备选假设H1:实际频次与期望频次有差别
其次:假设H0是成立的,基于假设计算出x2值(卡方值),x2值代表了实际频次与期望频次的偏离程度。最后:如果P很小(理论小于0.05),则说明实际与期望偏离程度较大,分布不同。
下面举例说明,卡方分布计算逻辑。
(1)卡方值计算公式:
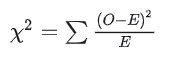
其中,O为实际频数,E为期望频数。期望频数是实际频数的期望值。对于r*c行列数,第r行第c列格子中观察频数 Orc。
Orc对应的期望频数为Erc=(Nr*Nc)/N
,其中 Nr为第r行的合计数,Nc为第c列的合计数,n为总样本量。
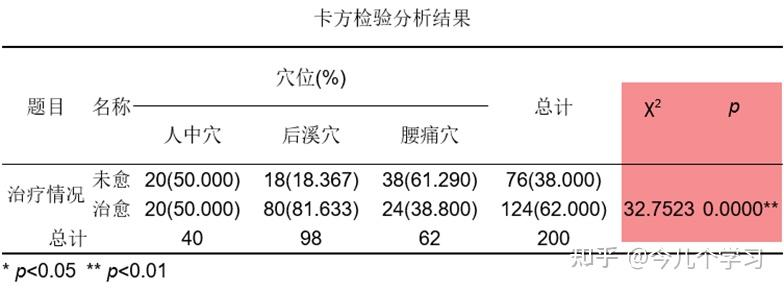
比如“人中穴未愈”的实际频数为20,期望频数=40*76/200=15.2,
“人中穴治愈”的实际频数为20,期望频数=40*124/200=24.8,其余计算类似。
(2)卡方值计算过程
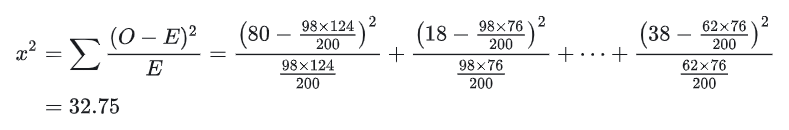
(3)计算自由度 df=(3-1)=2,根据自由度及显著性水平0.05查询对应临界值5.9915。比较临界值与统计值大小,32.75>5.9915,即统计量大于临界值,认为差异较显著,其他维度也采用同样的方式进行计算
(4)为了方便理解,将上述数据进行变形,整理格式如下:

(5)优劣势
优势1:相对其他方式,验证分布是否一致较为敏感。
方法劣势
- 卡方检验的频数只能以整数形式出现,相对指标不可用。
- 由于维度变化存在波浪效应,不同维度下的指标,很难源于同一分布。
- 不适合进行分布差异的量化。
该方法仅可用于判断两绝对指标的分布是否有差异,但如果需要量化度量各差异的程度,以及在各维度间进行比较,此方式不太适用
关注公众号「水沐教育科技」,在手机上阅读所有教程,随时随地都能学习。内含一款搜索神器,免费下载全网书籍和视频。

微信扫码关注公众号